Case Study 1 Delta Mush - Part 1
by Luca Di Sera
Introduction
Welcome the to the first part of the Delta Mush case study. We will dive into a first working, but completely and horribly unoptimized, version of the deformer.
Before starting there is a small disclaimer I’d like to write. It is important so bear the following in mind while reading or studying the code. As a first draft the code is not optimized in any way. Actually I’ve written it in a worse way than I would ( or should ) so as to be able to show some concepts in the following case study parts. Some choice are there to make the code more expressive so that you can more easily understand what we are doing. This has actually made the code a bit ugly for my taste. I’m not gonna refactor it for now ( even tough it needs it ) because we are going to have to restructure a lot of code and rethink how we store and pass around data and data structures when we will talk about data caching. There is some code replication, there are useless comments, some comments that should be there aren’t and so on… We are gonna change it slowly when we have a more representative structure. So please bear with it.
An important change
So, last time I said that we would use a method for calculating and applying the deltas that would need the mesh to have correctly unwrapped UVs. While I was writing the first version of the code I learned a new method that is pretty functional, easy to write, and interesting to experiment optimizations on. This new method doesn’t require UVs and it is better than the other non-UVs method I knew of. So this code uses this new method.
So, how does this method work? It has similarities with the method I explained last time. The difference is in how we build the tangent space representation mostly.
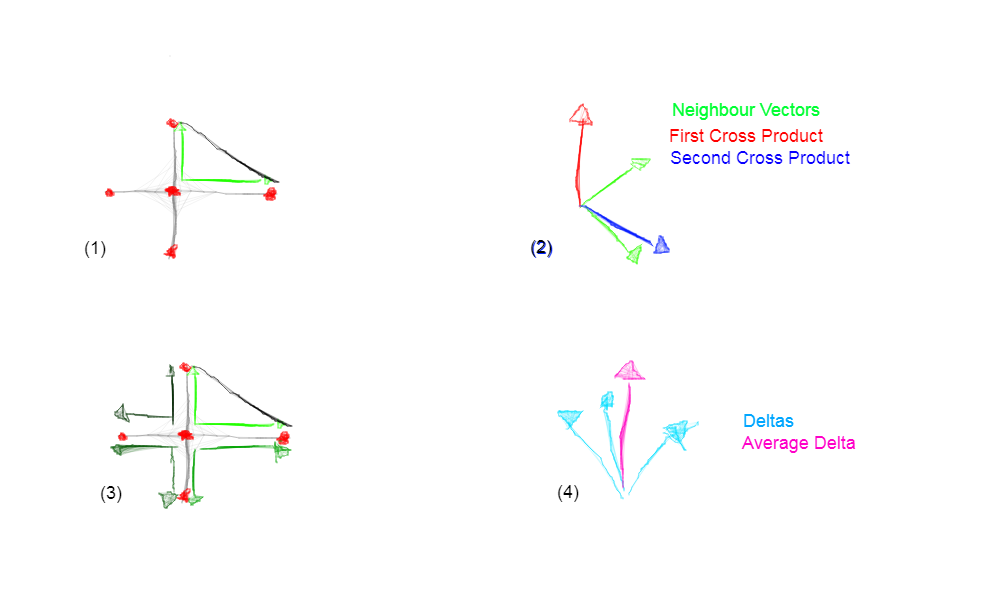
So, as you can see from the image (1), we will use the neighbour vertexes pairs to build two vectors that are relative to the vertex we are calculating for. Those will be the base of our tanget space. We will do a cross product to find an orthogonal axis. Since we could have a triangle that isn’t a right triangle to ensure the orghonality of all the axis we are going to do a second cross product to replace one of the two neighbour vectors (2). This will be done on every triangle we can build from the neighbours (3). We will have more than one delta with this process. In the end we average the deltas we’ve found to have the the final delta we need (4).
Now, calculating more than one delta is obviously slower. We could use only one triangle and use a single delta but we would have a less precise outcome. The algorithm to use depends on what you purposes are. For performance reason we could even implement both of them and let the user choose which one to use.
As you can see it is a simple method that will translate easily into code. This should be similar to how maya computes its tangent space. I had read a post about it somewhere but I can’t find it any more unfortunately.
Maya Boilerplate
First we will talk about some of the boilerplate code we have to write. We will then finally dive into the deform method.
Plugin Registration
// Copyright 2018 Luca Di Sera
// Contact: disera.luca@gmail.com
// https://github.com/diseraluca
// https://www.linkedin.com/in/luca-di-sera-200023167
//
// This code is licensed under the MIT License.
// More informations can be found in the LICENSE file in the root folder of this repository
//
//
// File : pluginMain.cpp
#include "DeltaMush.h"
#include <maya/MFnPlugin.h>
MStatus initializePlugin(MObject obj) {
MStatus status{};
MFnPlugin plugin{ obj, "Luca Di Sera", "1.0.0.0", "Any", &status };
CHECK_MSTATUS_AND_RETURN_IT(status);
status = plugin.registerNode(DeltaMush::typeName, DeltaMush::typeId, DeltaMush::creator, DeltaMush::initialize, MPxNode::kDeformerNode);
CHECK_MSTATUS_AND_RETURN_IT(status);
return MStatus::kSuccess;
}
MStatus uninitializePlugin(MObject obj) {
MStatus status{};
MFnPlugin plugin{ obj };
status = plugin.deregisterNode(DeltaMush::typeId);
CHECK_MSTATUS_AND_RETURN_IT(status);
return MStatus::kSuccess;
}
There isn’t much to explain here. We’re just registering the node and providing the .dll entry point. I’ve seen some people use string literals for the typeName but I like to keep everything under the class namespace.
DeltaMush header
// Copyright 2018 Luca Di Sera
// Contact: disera.luca@gmail.com
// https://github.com/diseraluca
// https://www.linkedin.com/in/luca-di-sera-200023167
//
// This code is licensed under the MIT License.
// More informations can be found in the LICENSE file in the root folder of this repository
//
//
// File : DeltaMush.h
//
// The DeltaMush class is a custom deformer for Autodesk Maya that implements
// the Delta Mush smoothing algorithm { "Delta Mush: smoothing deformations while preserving detail" - Joe Mancewicz, Matt L.Derksen, StudiosHans Rijpkema, StudiosCyrus A.Wilson }.
// This node will perform a Delta Mush smoothing that smooths a mesh while preventing the loss of volume and details.
// Used to help and speed up the skinning of rigs while giving high level and fast deformations.
// This implementation of the deformer requires a reference mesh that is an exact rest-pose copy of the deformed mesh.
#pragma once
#include <maya/MPxDeformerNode.h>
#include <maya/MPointArray.h>
#include <maya/MIntArray.h>
#include <maya/MVector.h>
#include <maya/MFnMesh.h>
#include <vector>
// An helper struct to store per-vertex deltas and their magnitude
struct deltaCache {
public:
MVectorArray deltas;
double deltaMagnitude;
};
class DeltaMush : public MPxDeformerNode {
public:
static void* creator();
static MStatus initialize();
virtual MStatus deform(MDataBlock & block, MItGeometry & iterator, const MMatrix & matrix, unsigned int multiIndex) override;
private:
// Get the neighbours vertices per-vertex of mesh. The neighbours indexes are stored into out_neighbours
MStatus getNeighbours(MObject& mesh, std::vector<MIntArray>& out_neighbours, unsigned int vertexCount) const;
// Perform an average neighbour smoothing on the vertices in vertices position and stores the smoothedPositions in out_smoothedPositions.
MStatus averageSmoothing(const MPointArray& verticesPositions, MPointArray& out_smoothedPositions, const std::vector<MIntArray>& neighbours, unsigned int iterations, double weight) const;
// Calculates and return an MVector representing the average positions of the neighbours vertices of the vertex with ID = vertexIndex
MVector neighboursAveragePosition(const MPointArray& verticesPositions, const std::vector<MIntArray>& neighbours, unsigned int vertexIndex) const;
// Calculate the tangent space deltas between the smoothed positions and the original positions and stores them in out_deltas.
MStatus cacheDeltas(const MPointArray& vertexPositions, const MPointArray& smoothedPositions, const std::vector<MIntArray>& neighbours, std::vector<deltaCache>& out_deltas, unsigned int vertexCount) const;
MStatus buildTangentSpaceMatrix(MMatrix& out_TangetSpaceMatrix, const MVector& tangent, const MVector& normal, const MVector& binormal) const;
public:
static MString typeName;
static MTypeId typeId;
static MObject referenceMesh;
static MObject smoothingIterations;
static MObject smoothWeight;
static MObject deltaWeight;
};
As you can see we don’t have much going on here. I’ve put a lot of methods to simplify the reading of the deform method. This has fractured the code in some places. I especially chose to pass many references around to keep the methods as generic as possible but I would actually move some memory to instance variables ( this would probably save some performance by removing the allocation of data we are doing and removing some refence pointers passing ) and read it from there.
deltaCache is an helper structure to store the per-vertex deltas we will calculate. But why are we storing the magnitude too? We will use it later to scale the final delta to the correct lenght to avoid the problems of precision losing and to be sure to have the correct lenght since we are modifying the vectors a lot.
We have a small amount of attributes ( some new ones will need to be added later tough ), nothing fancy, that we will se in the next section.
The initialize method
// Copyright 2018 Luca Di Sera
// Contact: disera.luca@gmail.com
// https://github.com/diseraluca
// https://www.linkedin.com/in/luca-di-sera-200023167
//
// This code is licensed under the MIT License.
// More informations can be found in the LICENSE file in the root folder of this repository
//
//
// File : DeltaMush.cpp
#include "DeltaMush.h"
#include <maya/MFnTypedAttribute.h>
#include <maya/MFnNumericAttribute.h>
#include <maya/MGlobal.h>
#include <maya/MItGeometry.h>
#include <maya/MItMeshVertex.h>
#include <maya/MFloatVectorArray.h>
#include <maya/MMatrix.h>
MString DeltaMush::typeName{ "ldsDeltaMush" };
MTypeId DeltaMush::typeId{ 0xd1230a };
MObject DeltaMush::referenceMesh;
MObject DeltaMush::smoothingIterations;
MObject DeltaMush::smoothWeight;
MObject DeltaMush::deltaWeight;
void * DeltaMush::creator()
{
return new DeltaMush();
}
MStatus DeltaMush::initialize()
{
MStatus status{};
MFnTypedAttribute tAttr;
MFnNumericAttribute nAttr;
referenceMesh = tAttr.create("referenceMesh", "ref", MFnData::kMesh, &status);
CHECK_MSTATUS_AND_RETURN_IT(status);
CHECK_MSTATUS(addAttribute(referenceMesh));
smoothingIterations = nAttr.create("smoothingIterations", "smi", MFnNumericData::kInt, 1, &status);
CHECK_MSTATUS_AND_RETURN_IT(status);
CHECK_MSTATUS(nAttr.setKeyable(true));
CHECK_MSTATUS(nAttr.setMin(1));
CHECK_MSTATUS(addAttribute(smoothingIterations));
smoothWeight = nAttr.create("smoothWeight", "smw", MFnNumericData::kDouble, 1.0, &status);
CHECK_MSTATUS_AND_RETURN_IT(status);
CHECK_MSTATUS(nAttr.setKeyable(true));
CHECK_MSTATUS(nAttr.setMin(0.0));
CHECK_MSTATUS(nAttr.setMax(1.0));
CHECK_MSTATUS(addAttribute(smoothWeight));
deltaWeight = nAttr.create("deltaWeight", "dlw", MFnNumericData::kDouble, 1.0, &status);
CHECK_MSTATUS_AND_RETURN_IT(status);
CHECK_MSTATUS(nAttr.setKeyable(true));
CHECK_MSTATUS(nAttr.setMin(0.0));
CHECK_MSTATUS(nAttr.setMax(1.0));
CHECK_MSTATUS(addAttribute(deltaWeight));
CHECK_MSTATUS(attributeAffects(referenceMesh, outputGeom));
CHECK_MSTATUS(attributeAffects(smoothingIterations, outputGeom));
CHECK_MSTATUS(attributeAffects(smoothWeight, outputGeom));
CHECK_MSTATUS(attributeAffects(deltaWeight, outputGeom));
MGlobal::executeCommand("makePaintable -attrType multiFloat -sm deformer ldsDeltaMush weights");
return MStatus::kSuccess;
}
Here again, we pretty much have all boilerplate code. We have a typedAttribute of type kMesh that is the mesh we will use as a refence. We expect this mesh to have the same topology as the deformed mesh and the same per-vertex ID. In simpler terms, it should be a bind-pose copy of the deformed mesh.
Then we have the number of iterations for the smoothing algorithm ( as we said before it will be a simple average smoothing ) and some weights for the smoothing and the delta application.
MGlobal::executeCommand("makePaintable -attrType multiFloat -sm deformer ldsDeltaMush weights");
If you have written a deformer before you should have seen this line of code. It is just us enabling the per-vertex weight for the deformer. It escapes me why there doesn’t exist an API method for this but we are constrained to use MEL commands. We should probably concatenate the typeName instead of writing it as a literal to keep the string references to zero so that we can change the name without breaking anything but it is just a small out-of-scope precaution for what we are currently doing.
Well, nothing difficult as you can see. Let’s finally dive to the real core of the delta mush.
The DeltaMush
MStatus DeltaMush::deform(MDataBlock & block, MItGeometry & iterator, const MMatrix & matrix, unsigned int multiIndex)
{
MStatus status{};
MPlug referenceMeshPlug{ thisMObject(), referenceMesh };
if (!referenceMeshPlug.isConnected()) {
MGlobal::displayWarning(this->name() + ": referenceMesh is not connected. Please connect a mesh");
return MStatus::kUnknownParameter;
}
// Retrieves attributes values
float envelopeValue{ block.inputValue(envelope).asFloat() };
MObject referenceMeshValue{ block.inputValue(referenceMesh).asMesh() };
int smoothingIterationsValue{ block.inputValue(smoothingIterations).asInt() };
double smoothWeightValue{ block.inputValue(smoothWeight).asDouble() };
double deltaWeightValue{ block.inputValue(deltaWeight).asDouble() };
int vertexCount{ iterator.count(&status) };
CHECK_MSTATUS_AND_RETURN_IT(status);
// Retrieves the positions for the reference mesh
MFnMesh referenceMeshFn{ referenceMeshValue };
MPointArray referenceMeshVertexPositions{};
referenceMeshVertexPositions.setLength(vertexCount);
CHECK_MSTATUS_AND_RETURN_IT(referenceMeshFn.getPoints(referenceMeshVertexPositions));
// Build the neighbours array
std::vector<MIntArray> referenceMeshNeighbours{};
getNeighbours(referenceMeshValue, referenceMeshNeighbours, vertexCount);
// Calculate the smoothed positions for the reference mesh
MPointArray referenceMeshSmoothedPositions{};
averageSmoothing(referenceMeshVertexPositions, referenceMeshSmoothedPositions, referenceMeshNeighbours, smoothingIterationsValue, smoothWeightValue);
// Calculate the deltas
std::vector<deltaCache> deltas{};
cacheDeltas(referenceMeshVertexPositions, referenceMeshSmoothedPositions, referenceMeshNeighbours, deltas, vertexCount);
MPointArray meshVertexPositions{};
iterator.allPositions(meshVertexPositions);
// Caculate the smoothed positions for the deformed mesh
MPointArray meshSmoothedPositions{};
averageSmoothing(meshVertexPositions, meshSmoothedPositions, referenceMeshNeighbours, smoothingIterationsValue, smoothWeightValue);
// Apply the deltas
MPointArray resultPositions{};
resultPositions.setLength(vertexCount);
for (unsigned int vertexIndex{ 0 }; vertexIndex < vertexCount; vertexIndex++) {
MVector delta{};
unsigned int neighbourIterations{ referenceMeshNeighbours[vertexIndex].length() - 1 };
for (unsigned int neighbourIndex{ 0 }; neighbourIndex < neighbourIterations; neighbourIndex++) {
MVector tangent = meshSmoothedPositions[referenceMeshNeighbours[vertexIndex][neighbourIndex]] - meshSmoothedPositions[vertexIndex];
MVector neighbourVerctor = meshSmoothedPositions[referenceMeshNeighbours[vertexIndex][neighbourIndex + 1]] - meshSmoothedPositions[vertexIndex];
tangent.normalize();
neighbourVerctor.normalize();
MVector binormal{ tangent ^ neighbourVerctor };
MVector normal{ tangent ^ binormal };
// Build Tangent Space Matrix
MMatrix tangentSpaceMatrix{};
buildTangentSpaceMatrix(tangentSpaceMatrix, tangent, normal, binormal);
// Accumulate the displacement Vectors
delta += tangentSpaceMatrix * deltas[vertexIndex].deltas[neighbourIndex];
}
// Averaging the delta
delta /= static_cast<double>(neighbourIterations);
// Scaling the delta
delta = delta.normal() * (deltas[vertexIndex].deltaMagnitude * deltaWeightValue);
resultPositions[vertexIndex] = meshSmoothedPositions[vertexIndex] + delta;
// We calculate the new definitive delta and apply the remaining scaling factors to it
delta = resultPositions[vertexIndex] - meshVertexPositions[vertexIndex];
float vertexWeight{ weightValue(block, multiIndex, vertexIndex) };
resultPositions[vertexIndex] = meshVertexPositions[vertexIndex] + (delta * vertexWeight * envelopeValue);
}
iterator.setAllPositions(resultPositions);
return MStatus::kSuccess;
}
As you can see the algorithm boils down to this 4 simple step, as said in the introduction:
- Smooth the rest pose mesh
- Calculate the Deltas for the smoothed rest pose mesh
- Smooth the deformation mesh
- Apply the delta back to the smoothed deformation mesh
That last big chunk of code is just us applying the delta. It does not reside in a method as I was testing some things and it isn’t worth it to refactor right now as we will change it a lot in the next parts.
Preparing some values we need
MStatus DeltaMush::deform(MDataBlock & block, MItGeometry & iterator, const MMatrix & matrix, unsigned int multiIndex)
{
MStatus status{};
MPlug referenceMeshPlug{ thisMObject(), referenceMesh };
if (!referenceMeshPlug.isConnected()) {
MGlobal::displayWarning(this->name() + ": referenceMesh is not connected. Please connect a mesh");
return MStatus::kUnknownParameter;
}
// Retrieves attributes values
float envelopeValue{ block.inputValue(envelope).asFloat() };
MObject referenceMeshValue{ block.inputValue(referenceMesh).asMesh() };
int smoothingIterationsValue{ block.inputValue(smoothingIterations).asInt() };
double smoothWeightValue{ block.inputValue(smoothWeight).asDouble() };
double deltaWeightValue{ block.inputValue(deltaWeight).asDouble() };
int vertexCount{ iterator.count(&status) };
CHECK_MSTATUS_AND_RETURN_IT(status);
// Retrieves the positions for the reference mesh
MFnMesh referenceMeshFn{ referenceMeshValue };
MPointArray referenceMeshVertexPositions{};
referenceMeshVertexPositions.setLength(vertexCount);
CHECK_MSTATUS_AND_RETURN_IT(referenceMeshFn.getPoints(referenceMeshVertexPositions));
// Build the neighbours array
std::vector<MIntArray> referenceMeshNeighbours{};
getNeighbours(referenceMeshValue, referenceMeshNeighbours, vertexCount);
Before coming to the first part of the algorithm, smoothing the reference mesh, wee have to prepare some data. First of all we check if we have an input mesh connected. Without one we could not make the deformer work ( this won’t be totally true later when we cache out data as we can work on the cached data without having referenceMesh connected and keep doing it until the need to rebind ). This warning will be printed as soon as the deformer is createad as, for now, we are not providing a command to use it and the user has to connect referenceMesh manually.
We get the value of all the attributes that we need. This is just normal administration. After that we store the current number of vertex. This will be used a lot. As we expect the two meshes to be the same we will use this same value for every calculation that needs it be it on the reference mesh or on the deformed mesh. As a design choiche we are not checking if this equality is true and just assume that the user uses a correct reference mesh. This is debatable, but for the purposes of this study it would just be a distraction to check.
We then prepare the data needed to work on the reference mesh. Just a note here, that you probably already know, but setting the needed lenght and getting all the points in one go is a lot faster that dynamically reallocating memory ( that is a costly operation ) and getting them one by one. Lastly, before we can finally get to the smoothing, we get and store the per-vertex neighbours indeces to use later.
The getNeighbours method has the following, pretty simple, implementation:
MStatus DeltaMush::getNeighbours(MObject & mesh, std::vector<MIntArray>& out_neighbours, unsigned int vertexCount) const
{
out_neighbours.resize(vertexCount);
MItMeshVertex meshVtxIt{ mesh };
for (unsigned int vertexIndex{ 0 }; vertexIndex < vertexCount; vertexIndex++, meshVtxIt.next()) {
CHECK_MSTATUS_AND_RETURN_IT(meshVtxIt.getConnectedVertices(out_neighbours[vertexIndex]));
}
return MStatus::kSuccess;
}
As you can see it is a pretty simple method, Maya does the work for us and we just have to provide some containers. One thing to note, is that we should delete the MStatus check in the loop for performance reasons. But for now we can leave it there.
Finally we can get to the first point of our list. The smoothing.
Average Smoothing
// Calculate the smoothed positions for the reference mesh
MPointArray referenceMeshSmoothedPositions{};
averageSmoothing(referenceMeshVertexPositions, referenceMeshSmoothedPositions, referenceMeshNeighbours, smoothingIterationsValue, smoothWeightValue);
I wrapped this in a method that has the following implementation:
MStatus DeltaMush::averageSmoothing(const MPointArray & verticesPositions, MPointArray & out_smoothedPositions, const std::vector<MIntArray>& neighbours, unsigned int iterations, double weight) const
{
unsigned int vertexCount{ verticesPositions.length() };
out_smoothedPositions.setLength(vertexCount);
// A copy is necessary to avoid losing the original data trough the computations while working iteratively on the smoothed positions
MPointArray verticesPositionsCopy{ verticesPositions };
for (unsigned int iterationIndex{ 0 }; iterationIndex < iterations; iterationIndex++) {
for (unsigned int vertexIndex{ 0 }; vertexIndex < vertexCount; vertexIndex++) {
MVector averagePosition{ neighboursAveragePosition(verticesPositionsCopy, neighbours, vertexIndex) };
MVector smoothedPosition{ ((averagePosition - verticesPositionsCopy[vertexIndex]) * weight) + verticesPositionsCopy[vertexIndex] };
out_smoothedPositions[vertexIndex] = smoothedPosition;
}
verticesPositionsCopy.copy(out_smoothedPositions);
}
return MStatus::kSuccess;
}
To recap, the simple smoothing we are doing here is an additive smoothing that calculates the smoothed position for iteration n as the average position, as of iteration n-1, of the neighbour verteces.
As you can see this type of simple smoothing can be done in a few lines of code. The only “tricky” part here is that we have to make a copy of the data for the following iterations. Since we could be accessing a vertex more than one time ( for example vertex 64 and vertex 1 may be neighbours ) we have to keep the original and n-1 iteration data intact so that we won’t work on the wrong set of data. If we didn’t we could end up working with an asynchronous data set, with some vertex on iteration n, other on interation n+1 or others that are a mix of n-iteration positions and n-1 iteration positions. Now, this isn’t always necessary, but we will look into optimizing how we use and reuse data later on.
neighboursAveragePosition is implemented as follow:
MVector DeltaMush::neighboursAveragePosition(const MPointArray & verticesPositions, const std::vector<MIntArray>& neighbours, unsigned int vertexIndex) const
{
unsigned int neighbourCount{ neighbours[vertexIndex].length() };
MVector averagePosition{};
for (unsigned int neighbourIndex{ 0 }; neighbourIndex < neighbourCount; neighbourIndex++) {
averagePosition += verticesPositions[neighbours[vertexIndex][neighbourIndex]];
}
averagePosition /= neighbourCount;
return averagePosition;
}
This is self explanatory. We are just accumulating the positions of the neighbours and averaging them. This is it. The smoothing part, as you can see, is as simple as it gets. Let’s move on.
Calculating the deltas
// Calculate the deltas
std::vector<deltaCache> deltas{};
cacheDeltas(referenceMeshVertexPositions, referenceMeshSmoothedPositions, referenceMeshNeighbours, deltas, vertexCount);
This is wrapped up in a method. It is called cacheDeltas because we should actually cache them since they’re non-changing data. But we will look into it in the next part.
MStatus DeltaMush::cacheDeltas(const MPointArray & vertexPositions, const MPointArray & smoothedPositions, const std::vector<MIntArray>& neighbours, std::vector<deltaCache> & out_deltas, unsigned int vertexCount) const
{
out_deltas.resize(vertexCount);
for (unsigned int vertexIndex{ 0 }; vertexIndex < vertexCount; vertexIndex++) {
MVector delta{ vertexPositions[vertexIndex] - smoothedPositions[vertexIndex] };
out_deltas[vertexIndex].deltaMagnitude = delta.length();
unsigned int neighbourIterations{ neighbours[vertexIndex].length() - 1 };
out_deltas[vertexIndex].deltas.setLength(neighbourIterations);
for (unsigned int neighbourIndex{ 0 }; neighbourIndex < neighbourIterations; neighbourIndex++) {
MVector tangent = smoothedPositions[neighbours[vertexIndex][neighbourIndex]] - smoothedPositions[vertexIndex];
MVector neighbourVerctor = smoothedPositions[neighbours[vertexIndex][neighbourIndex + 1]] - smoothedPositions[vertexIndex];
tangent.normalize();
neighbourVerctor.normalize();
MVector binormal{ tangent ^ neighbourVerctor };
MVector normal{ tangent ^ binormal };
// Build Tangent Space Matrix
MMatrix tangentSpaceMatrix{};
buildTangentSpaceMatrix(tangentSpaceMatrix, tangent, normal, binormal);
// Calculate the displacement Vector
out_deltas[vertexIndex].deltas[neighbourIndex] = tangentSpaceMatrix.inverse() * delta;
}
}
return MStatus::kSuccess;
}
As you can see this one turns out to be a simple method too. As explained before, we are calculating a tangent space delta for every neighbours pair.
MVector delta{ vertexPositions[vertexIndex] - smoothedPositions[vertexIndex] };
out_deltas[vertexIndex].deltaMagnitude = delta.length();
As explained in the introduction to this case study:
The idea here is that if the smoothing of the mesh ( in its original position - The bind pose ) produced a certain loss of volume
the smoothing of the deformed mesh will produce a similar amount of loss. By reapplying the delta we are trying to get as near as
possible to the original position of the vertex.
Here we are, then, finding the displcement vector of this volume loss, going from the smoothed position of the vertex to the initial position of the vertex. When we will apply this delta we will get as near as possible to the original volume of the mesh. We then store its magnitude to rescale the final delta later.
unsigned int neighbourIterations{ neighbours[vertexIndex].length() - 1 };
We then start to iterate over the vertex pairs. Now, since we are iterating over pairs and not single elements, the number of iterations we have to do is reduced by one. This is because we are going to eat the last element with the penultimate element and by iterating on all the elements we would go out of the array bounds. This is easily seen in the image:
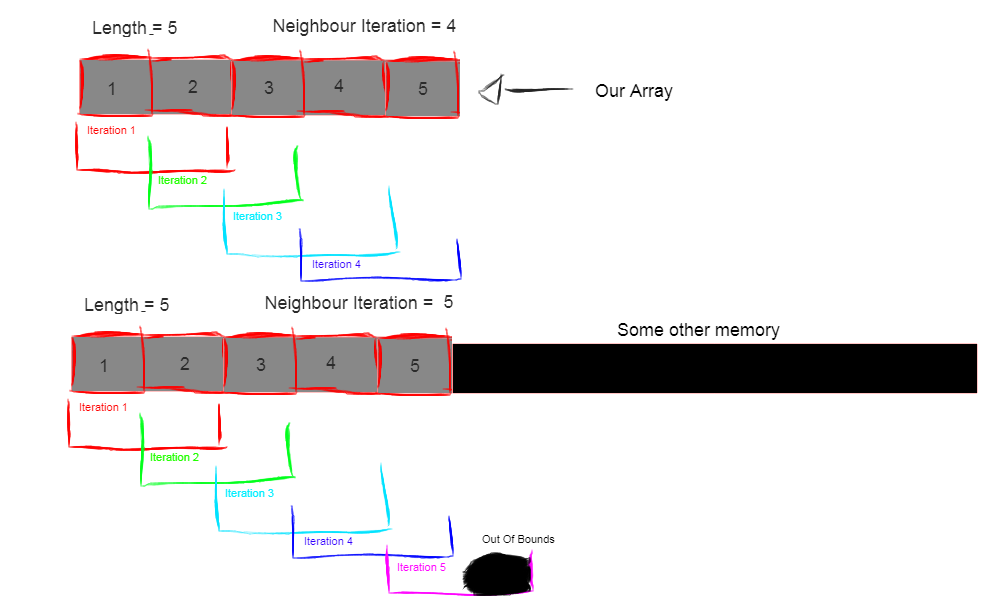
unsigned int neighbourIterations{ neighbours[vertexIndex].length() - 1 };
out_deltas[vertexIndex].deltas.setLength(neighbourIterations);
for (unsigned int neighbourIndex{ 0 }; neighbourIndex < neighbourIterations; neighbourIndex++) {
MVector tangent = smoothedPositions[neighbours[vertexIndex][neighbourIndex]] - smoothedPositions[vertexIndex];
MVector neighbourVerctor = smoothedPositions[neighbours[vertexIndex][neighbourIndex + 1]] - smoothedPositions[vertexIndex];
tangent.normalize();
neighbourVerctor.normalize();
MVector binormal{ tangent ^ neighbourVerctor };
MVector normal{ tangent ^ binormal };
// Build Tangent Space Matrix
MMatrix tangentSpaceMatrix{};
buildTangentSpaceMatrix(tangentSpaceMatrix, tangent, normal, binormal);
// Calculate the displacement Vector
out_deltas[vertexIndex].deltas[neighbourIndex] = tangentSpaceMatrix.inverse() * delta;
This is what we do for each pair of neighbours. We have to build our tangent space matrix. As said at the start of this post we find ourselves two vectors from the current vertex to two of their neighbours. The one I called tangent is the one I will use as is. Here we work with normalized vectors, we first do a cross product to find an axis tangent to the two vertices. The second cross product is to ensure orthogonality, as said before.
buildTangentSpaceMatrix is there to make the code more readable and is implemented as follows:
MStatus DeltaMush::buildTangentSpaceMatrix(MMatrix & out_TangetSpaceMatrix, const MVector & tangent, const MVector & normal, const MVector & binormal) const
{
// M = [tangent, normal, bitangent, zeroed-translation]
out_TangetSpaceMatrix[0][0] = tangent.x;
out_TangetSpaceMatrix[0][1] = tangent.y;
out_TangetSpaceMatrix[0][2] = tangent.z;
out_TangetSpaceMatrix[0][3] = 0.0;
out_TangetSpaceMatrix[1][0] = normal.x;
out_TangetSpaceMatrix[1][1] = normal.y;
out_TangetSpaceMatrix[1][2] = normal.z;
out_TangetSpaceMatrix[1][3] = 0.0;
out_TangetSpaceMatrix[2][0] = binormal.x;
out_TangetSpaceMatrix[2][1] = binormal.y;
out_TangetSpaceMatrix[2][2] = binormal.z;
out_TangetSpaceMatrix[2][3] = 0.0;
out_TangetSpaceMatrix[3][0] = 0.0;
out_TangetSpaceMatrix[3][1] = 0.0;
out_TangetSpaceMatrix[3][2] = 0.0;
out_TangetSpaceMatrix[3][3] = 1.0;
return MStatus::kSuccess;
}
As you can see we’re just assigning the values manually to where they belong. There are cleaner ways to write this matrix but we will change how we work with this data in the future so we’ll leave it like that.
out_deltas[vertexIndex].deltas[neighbourIndex] = tangentSpaceMatrix.inverse() * delta;
Having the tangent space matrix and having the delta, we apply the inverse of the matrix to the delta and store it for later use.
Smoothing the deformed mesh
MPointArray meshVertexPositions{};
iterator.allPositions(meshVertexPositions);
// Caculate the smoothed positions for the deformed mesh
MPointArray meshSmoothedPositions{};
averageSmoothing(meshVertexPositions, meshSmoothedPositions, referenceMeshNeighbours, smoothingIterationsValue, smoothWeightValue);
Most of the code in the second part of the deformer is the same as the first. Here we smooth the mesh like we did for the reference one. Nothing to say here.
Finally applying the deltas back
// Apply the deltas
MPointArray resultPositions{};
resultPositions.setLength(vertexCount);
for (unsigned int vertexIndex{ 0 }; vertexIndex < vertexCount; vertexIndex++) {
MVector delta{};
unsigned int neighbourIterations{ referenceMeshNeighbours[vertexIndex].length() - 1 };
for (unsigned int neighbourIndex{ 0 }; neighbourIndex < neighbourIterations; neighbourIndex++) {
MVector tangent = meshSmoothedPositions[referenceMeshNeighbours[vertexIndex][neighbourIndex]] - meshSmoothedPositions[vertexIndex];
MVector neighbourVerctor = meshSmoothedPositions[referenceMeshNeighbours[vertexIndex][neighbourIndex + 1]] - meshSmoothedPositions[vertexIndex];
tangent.normalize();
neighbourVerctor.normalize();
MVector binormal{ tangent ^ neighbourVerctor };
MVector normal{ tangent ^ binormal };
// Build Tangent Space Matrix
MMatrix tangentSpaceMatrix{};
buildTangentSpaceMatrix(tangentSpaceMatrix, tangent, normal, binormal);
// Accumulate the displacement Vectors
delta += tangentSpaceMatrix * deltas[vertexIndex].deltas[neighbourIndex];
}
// Averaging the delta
delta /= static_cast<double>(neighbourIterations);
// Scaling the delta
delta = delta.normal() * (deltas[vertexIndex].deltaMagnitude * deltaWeightValue);
resultPositions[vertexIndex] = meshSmoothedPositions[vertexIndex] + delta;
// We calculate the new definitive delta and apply the remaining scaling factors to it
delta = resultPositions[vertexIndex] - meshVertexPositions[vertexIndex];
float vertexWeight{ weightValue(block, multiIndex, vertexIndex) };
resultPositions[vertexIndex] = meshVertexPositions[vertexIndex] + (delta * vertexWeight * envelopeValue);
}
iterator.setAllPositions(resultPositions);
Here again we have a lot of repeated code. First thing first we have to buid our matrices again. This time, tough, we are going to apply it to our stored deltas, one by one, which we accumulate into a vector and then average.
// Accumulate the displacement Vectors
delta += tangentSpaceMatrix * deltas[vertexIndex].deltas[neighbourIndex];
}
// Averaging the delta
delta /= static_cast<double>(neighbourIterations);
After this most of the work is done. finally have our delta to apply. There is a problem. The direction of the vector is most surely correct, but its magnitude is not.
// Scaling the delta
delta = delta.normal() * (deltas[vertexIndex].deltaMagnitude * deltaWeightValue);
resultPositions[vertexIndex] = meshSmoothedPositions[vertexIndex] + delta;
This is where our stored magnitude comes for help. By normalizing the vector, thus giving us a vector of lenght one, and then multiplying it by the original magnitude, we are scaling it back to its original length. Nothing more simple! Here we apply our weight value to modify our scaling factor. If we had a 0.5 deltaWeightValue we would apply only half of our scaling factor - Thus getting back a delta only half as long as the original one.
We then apply this displacement to the position of the smoothed vertex ( remember that our deltas reinflate the smoothed vertex in the direction of the original vertex position ) to find our final position. And this is it, this is a working DeltaMush deformer. But we have a little fiddling left to do…
Applying per-vertex weight and the global envelope value
// We calculate the new definitive delta and apply the remaining scaling factors to it
delta = resultPositions[vertexIndex] - meshVertexPositions[vertexIndex];
float vertexWeight{ weightValue(block, multiIndex, vertexIndex) };
resultPositions[vertexIndex] = meshVertexPositions[vertexIndex] + (delta * vertexWeight * envelopeValue);
This too is mostly self-explaining. Now that we have our final position we can apply those post-deformation weights to it. To do this we get us a displacement vector from our original position to our final position. And then scale it relative to the envelope and the per-vertex weight. By adding this scaled delta to the original position we find our (for real this time) final position that is between the original deformed mesh and the DeltaMush one.
Conclusion
So, this has been a long post. I hope the code is clear enough. I expect people reading this to have, at least, a basic understanding of Maya API and MPxDeformerNodes. As you’ve seen the DeltaMush itself is not too difficult to implement. Having said that, it is a great mid-level deformer exercise that will give us so many possibilities for interesting optimizations and experiments. Before going, I will leave you with some data about the “speed” of this current version. I won’t talk about test scenes and so on because we will see them the next time when we will compare two versions of this deformer but to understand how slow it is this is run on a single 478402 vertices cylinder. The time is expressed in microseconds.
| Scene | AverageSample | MinSample | MaxSample |
|---|---|---|---|
| Single Cylinder | 92892042 | 91532793 | 95571787 |
As you can see, it’s terrible. But don’t worry we will start making it better next time when we will talk about Data Caching. We have endless possibilities for optimizing this code, and a long way ahead of us, but don’t worry the exciting part is gonna start soon.