Case Study 1 Delta Mush - Introduction

22 July 2018

by Luca Di Sera

Dulta mas… Delta mua… Delta uh??

In this first Case Study we are going to build a basic Delta Mush deformer and study some optimization technique on it. But what is a Delta Mush?

The Delta Mush algorithm is a smoothing algorithm that aims to reduce the time needed for production level skinning by cleaning up undesirable deformations. It was developed at Rhythm & Hues studios ( which unfortunaly has signed bankruptcy a few years ago ) and then became popular as a production level tool. The algorithm itself isn’t much difficult, which is a plus, but delivers great results and cuts production times.

The original paper Joe Mancewicz, Matt L. Derksen, and Cyrus A. Wilson, Delta mush: smoothing deformations while preserving detail can be found at ACM Digital Library and is a great read for those interested.

Here you can see an example of it in action ( and oh, boy is it wonderful ).

But how does it work? Well, it is actually simpler than it seems. The algorithm is divided in two main parts.

The smoothing

The first part of the algorithm is the smoothing part ( not so surprising uh? ). The Delta Mush usually uses weighted Laplacian Smoothing. Formally it is the defined per-vertex as such:

$\begin{align*} x_i = \sum{j=1}^N w_jp_j \end{align*}$

Where $N$ is number of connected vertices to vertex $i$ , $p_j$ are the position in space of the connected vertices and $x_i$ is the resulting position of vertex $i$ . $w_j$ is a weight factor that is applied to the transformation. It can be constant or it can be calculated from a series of factors. One techniques is to use the lenght of the edge between vertex $i$ and vertex $j$ to find an inversely proportional weight. In this Case Study we’ll keep it simple(r) and use a basic smoothing where we find the average position of the connected vertexes and displace the vertex to it.

$An example of a smoothing algorithm. Left - Non Smoothed Mesh \ Right - Smoothed Mesh$

Those smoothing algorithms usually lets the user decide a number of iterations to perform. Let $N$ be the number of iterations to perform, the 0 < $n$ < $N$ iteration is performed on the corresponding mesh that is smoothed $n-1$ times. In simpler terms, the smoothing is additive with subsequent iterations performed on the already smoothed mesh and not on the original mesh.

Now, these kind of smoothing algorithms produce loss of volume and details. Delta Mush performs a second operation to resolve this issue.

The delta in Delta Mush

How can we prevent this loss of volume and detail? Well, Delta Mush gives us a simple solution by using the smoothed deltas. What are those? A delta is non-other than a difference between two related values. In the Delta Mush case the delta is a vector in tangent space going from the final smoothed position of a vertex to the original position of the vertex in tangent space. Those deltas will then be reapplied to the deformed mesh to regain the lost volume. The idea here is that if the smoothing of the mesh ( in its original position - The bind pose ) produced a certain loss of volume the smoothing of the deformed mesh will produce a similar amount of loss. By reapplying the delta we are trying to get as near as possible to the original position of the vertex.

There is a problem tough. If the mesh is deformed, and we apply the deltas, we may find that we are displacing the vertexes in the wrong direction. That is because the displacement of the smoothing may have changed its orientation. Here comes the aforementioned tangent space to save the day.

Tangent Space

So, tangent space is a somewhat complex concept. But for our purposes we can try and simplify it a bit. In essence Tangent Space is a coordinate system relative to a certain surface where up is directly away from the surface ( how a normal would be for example ). In our case, we have to build this space relative to every vertex so that we can store and reapply the deltas correctly independant of how the vertices are transformed.

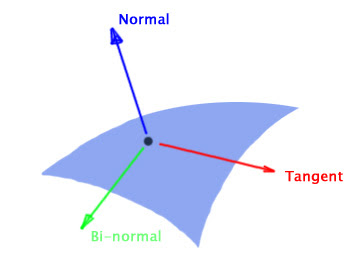
Tangent Space

As you can see from the image we can build it using the normal, the tangent and the binormal ( Maya API provides them for us trough MFnMesh using the UV of the mesh. I know of another method to build tangent space that doesn’t need UVs but we are probably gonna use Maya API directly in the code. We could end up trying to do it manually in the future if the API method ends up being a source of slowness ).

From these pieces we can build the following transformation matrix:

$\begin{align*} R_i = [t_i, n_i, b_i, s_i] \end{align*}$

where $t_i$ , $n_i$ , $b_i$ , $s_i$ are the tangent, the normal, the binormal, and the smoothed position of vertex $i$ . Trough applying the inverse of this matrix we can find a vector $v_i$ , that is the displacement of the vertex (AKA the delta), as follows:

$\begin{align*} v_i = {R_i}^{-1}p_i \end{align*}$

where $p_i$ is the original position of the vertex. This first pass is done on the original mesh in rest position ( we will cache this deltas in the end since they don’t change and needs to be calculated only once ). After we have deformed the mesh and smoothed it we can build a second transformation matrix as follows:

$\begin{align*} C_i = [t_i^{'}, n_i', b_i', s_i^{'}] \end{align*}$

where $t_i^{'}$ , $n_i'$ , $b_i'$ , $s_i^{'}$ are the tangent, normal, binormal and smoothed position of vertex $i$ in a deformed state. Trough this matrix ( which represents tangent space transformations ) we can find the final position $d_i$ of vertex $i$ by applying the transformation to $v_i$ :

$\begin{align*} d_i = C_iv_i \end{align*}$

Closing up

Now this may seem more difficult than it actually is to you. I haven’t properly explained many things and supposed that you already knew at least some concepts ( like what a coordinate system is or transformation matrices ) but all will be more clear when we will put our hands on some code. To recap, in an easier to understand way, the Delta Mush deformer is performed as follows:

Smooth the rest pose mesh
Calculate the Deltas for the smoothed rest pose mesh
Smooth the deformation mesh
Apply the delta back to the smoothed deformation mesh

It is as simple as that. Next time we will dive directly into the code of a first, completely unoptimized, version of a Delta Mush Deformer and finally dirty our hands a bit. See you next time.